| View previous topic :: View next topic |
| Author |
Message |
ZeroAssoluto
Joined: 05 Feb 2017
Posts: 942
Location: Rimini, Italy
|
 Posted: Sun Aug 15, 2021 9:44 am Post subject: Aug 15 VH Posted: Sun Aug 15, 2021 9:44 am Post subject: Aug 15 VH |
 |
|
Hi everyone,
| Code: |
+----------------+---------------+----------------+
| 8 79 679 | 2 367 4 | 36 5 1 |
| 1 2 46 | 8 36 5 | 7 349 3469 |
| 47 3 5 | 67 1 9 | 468 48 2 |
+----------------+---------------+----------------+
| 3479 4789 2 | 379 5 3678 | 3468 1 3468 |
| 349 1 489 | 39 2 368 | 5 7 3468 |
| 5 6 78 | 1 4 378 | 9 2 38 |
+----------------+---------------+----------------+
| 2 4789 4789 | 5 789 37 | 1 6 3489 |
| 679 789 3 | 4 6789 1 | 2 89 5 |
| 469 5 1 | 36 689 2 | 348 3489 7 |
+----------------+---------------+----------------+
|
Play this puzzle online at the Daily Sudoku site
| Quote: | W-Wing 3,6 in r2c5,r9c4 SL with number 3 in r29c8 and -6 in r3c4,r89c5
or
W-Wing 3,6 in r1c7,r2c5 SL with number 6 in r3c47 and -3 in r1c5,r2c89
or
XY-Wing 4,6,7 in r2c3,r3c14 and -6 in r2c5 |
Ciao Gianni |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Tue Aug 17, 2021 5:58 pm Post subject: Posted: Tue Aug 17, 2021 5:58 pm Post subject: |
 |
|
r2c5 can't be 6 because if you do then r2c3 is 4 and then r3c1 is 7 and r3c4 is 6.
This gives two 6's in block 2 so r2c5 <>6. |
|
| Back to top |
|
 |
TomC
Joined: 30 Oct 2020
Posts: 358
Location: Wales
|
 Posted: Tue Aug 17, 2021 6:32 pm Post subject: Posted: Tue Aug 17, 2021 6:32 pm Post subject: |
 |
|
| Mogulmeister wrote: | r2c5 can't be 6 because if you do then r2c3 is 4 and then r3c1 is 7 and r3c4 is 6.
This gives two 6's in block 2 so r2c5 <>6. |
Is this an XY wing? |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Tue Aug 17, 2021 8:04 pm Post subject: Posted: Tue Aug 17, 2021 8:04 pm Post subject: |
 |
|
No Tom, although as you have noted, it used the same cells as the XY Wing (sometimes just called a Y wing).
However the execution is different. This is a “Forcing Chain” that creates a contradiction showing that the initial assumption is wrong. It involves plugging in an actual value.
The XY wing is a logical structure that doesn’t care about the values that the cells might eventually take. The internal logic is saying that one end (pincer) or the other (r2c3 or r3c4) must be 6 which means there can be no 6 in r2c5.
The XY wing is of course just the shortest XY chain. Some people refer to them as “bent triples”
Last edited by Mogulmeister on Wed Aug 18, 2021 7:12 am; edited 1 time in total |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
|
| Back to top |
|
 |
TomC
Joined: 30 Oct 2020
Posts: 358
Location: Wales
|
 Posted: Wed Aug 18, 2021 1:17 pm Post subject: Posted: Wed Aug 18, 2021 1:17 pm Post subject: |
 |
|
I've been under the impression for a very long time that this was the way to solve XY wings. When I find the 3 candidate cells the contradiction is what is most apparent to me.
Is a W wing a form of forcing chain too? |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Aug 18, 2021 1:56 pm Post subject: Posted: Wed Aug 18, 2021 1:56 pm Post subject: |
 |
|
The classical use of "wings" is to produce a situation where one or other of the ends (pincers) contains the number which will cause the elimination. The situation works because one or other of the ends will always be true for that number.
| Quote: | | An XY-Wing is really a short XY-Chain that is described as a pattern and thus can be found more easily. We start by looking for a bivalue cell (the pivot). The possible candidates in that cell are called X and Y. Now we try to find two other cells that see the pivot (the pincers). One of those cells contains candidates X and Z (Z is an arbitrary candidate different from X and Y) and the other candidates Y and Z. Now Z can be eliminated from any cell that sees both pincers. |
Where a wing structure exists, you don't need to force a contradiction to determine the right or wrong value.
Any "wing" works with this mechanism. You don't know which end will remove the candidate but it has to be one or the other. The W wing has a slightly different construction, two bivalue cells, each containing the elimination candidate are joined by a strong link (SL).
| Quote: | | W-Wings are easy to spot and often very efficient. They consist of two bivalue cells with the same candidates, that are connected by a strong link on one of the candidates. The other candidate can be eliminated from all cells seeing both bivalue cells. Since a W-Wing is a chain internally, a prove of the logic written in plain text, as can be seen below, is complicated. The pattern itself, however, is easy to spot (filters can be a great help here). |
You don't need a contradiction for a wing to work.
A contradiction means you plug a number in to test the validity of your choice. When you create a contradiction you know that if the value chosen makes an impossible result then your alternative is correct. You will have noticed that dongrave uses the contradiction method with his excellent chains to solve some of the harder puzzles.
Last edited by Mogulmeister on Wed Aug 18, 2021 2:33 pm; edited 6 times in total |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Aug 18, 2021 2:07 pm Post subject: Posted: Wed Aug 18, 2021 2:07 pm Post subject: |
 |
|
On a general point everyone sees a puzzle differently which is why I put in the contradiction in after Gianni's XY wing. All wings are also chains. Not only is the XY Wing a chain but it is also an ALS xz. Using exactly the same squares.
ALS
Set A {4,6,7) r2c3 and r3c1
Set B {6,7} r3c4
Restricted common is 7 in r3c14
Common candidate to be removed is the 6 in r2c5 because it can see all other 6's in Set A&B.
Last edited by Mogulmeister on Wed Aug 18, 2021 2:25 pm; edited 1 time in total |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Aug 18, 2021 2:23 pm Post subject: Posted: Wed Aug 18, 2021 2:23 pm Post subject: |
 |
|
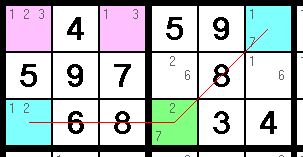
The classic XY wing above {1,2,7} has three candidates and most importantly 1 in both pincers (pale blue). The green square is the pivot that links them.
We don't know what values the blue squares will be but we can see that that one of them will have to be 1. Any 1(pink) that can be seen by both pincers is eliminated. You don't have to see a contradiction for the wing to work.
Diagram below is an XY chain at work that just happens to be a W Wing.
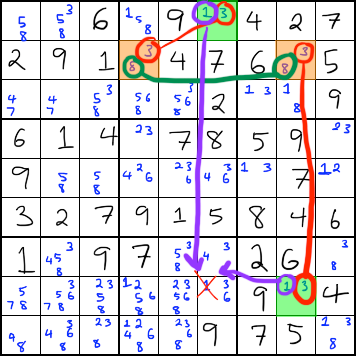
Last edited by Mogulmeister on Wed Aug 18, 2021 3:24 pm; edited 3 times in total |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Aug 18, 2021 3:03 pm Post subject: Posted: Wed Aug 18, 2021 3:03 pm Post subject: |
 |
|
Finally, on a philosophical point regarding Sudoku solving:

There are some who see strange "yellow" teeth in a black mouth rather than the famous symbol! |
|
| Back to top |
|
 |
|





